数学在前端动画中的应用

有时候你希望能回到过去，告诉年轻的自己，数学确实很重要! 但我怀疑自己当时会不会听进去…

前言

三角函数、两点间的距离，还有各种图形、角度计算公式，每每听到这些词语，就放佛回到了高中时代，想起了数学课本上那一道道让人头疼的数学题。在前端开发领域中，数学同样占据着举足轻重的地位，每次当视觉交互设计师提出，能不能按照这样那样的交互方式进行开发的时候，我时常会感觉力不从心。对于动画效果，实现的方式主要有css和js两种，为了做出更高质量的动画效果，通常需要借助一些数学知识来解决，本文主要结合三角函数在前端动画中的应用进行介绍。

三角函数介绍

三角函数，学生时代肯定学过，是以角度（数学上最常用弧度制）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数，在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。通过三角函数，我们可以获取到有规律的周期数据，在一个周期内，物体的运动是按照一种有规律的方式进行的，物体元素都是可以按照这个方式进行周期性运动的，进而可以让整个动画效果看起来更符合人类的视觉审美。

要想介绍三角函数，首先离不开当初学过的一个直角三角形：

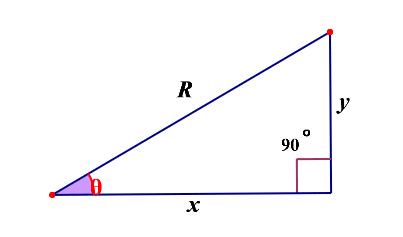
勾股定理的基本思想就是：两条直角边的平方和等于斜边平方和；由勾股定理进行推导即可得知，三角函数主要是代表边与角之间的关系；我给大家介绍其中的三种，其实还有很多，我们主要平时用的时候用这三个就够了：

正弦：sin(θ) = y / R

余弦：cos(θ) = x / R

正切：tan(θ) = y / x

这里我们以正弦函数为例进行演示，下图主要是一个正弦曲线图，对应的正弦曲线公式为：y = A sin(Bx + C) + D；

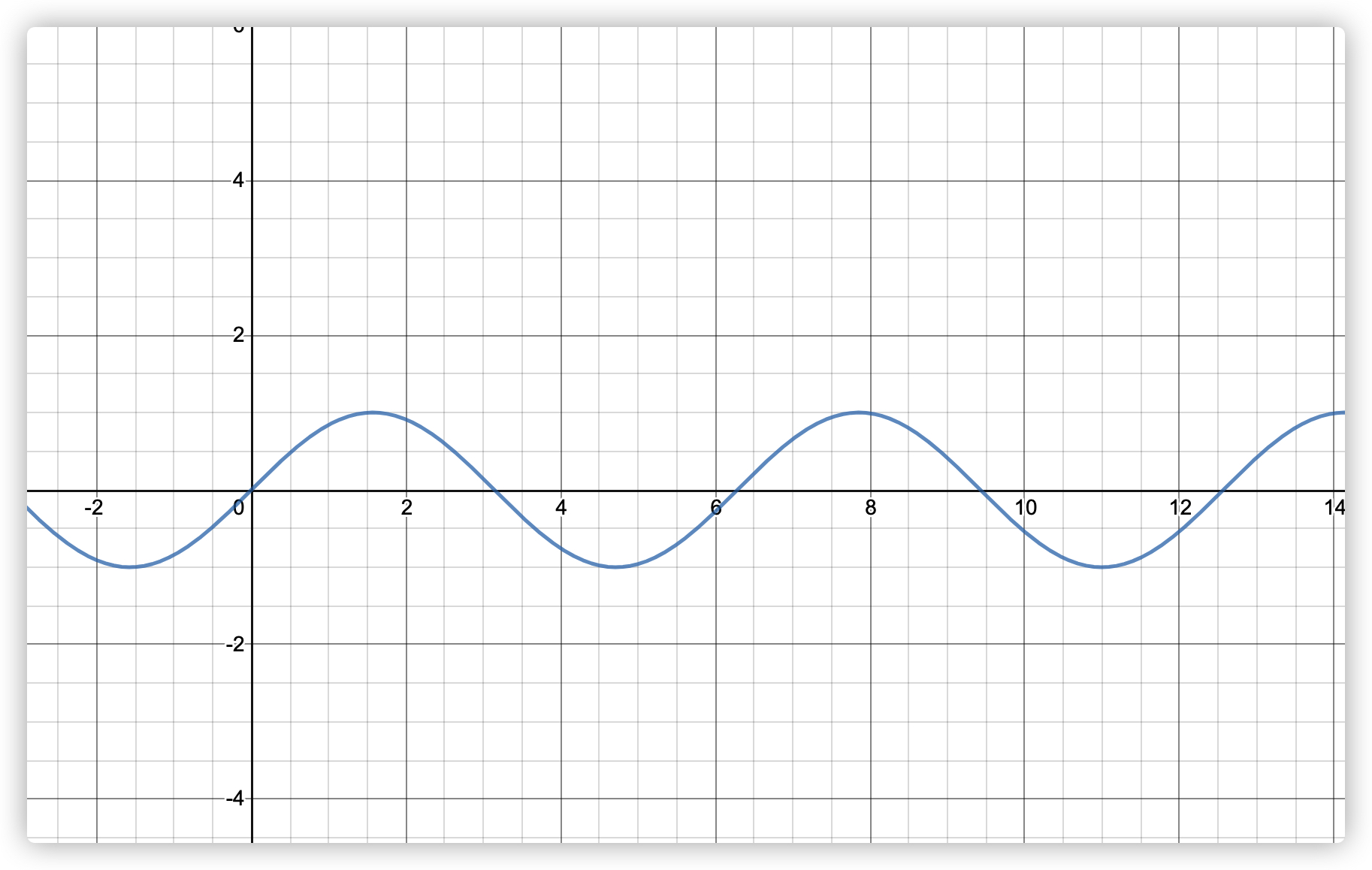
正弦参数概念

A 控制振幅，A 值越大，整体振幅越大，A 值越小，整体振幅越小；
B 值会影响周期，B 值越大，周期会相应的变小，B 值越小，周期会相应的变大。
C 值会影响图像左右移动，C 值为正数，图像右移像素，C 值为负数，图像左移像素。
D 值控制整个图像的上下移动。

三角函数在js中的对应

Math.sin(弧度)
Math.cos(弧度)
Math.tan(弧度）

<注意> 在js中用弧度代替角度，在浏览器中是不能识别角度的，只能用弧度来进行转换。

弧度是什么？

如果一弧度等于半径;那么整个圆的弧度= . =

整个圆的角度是360度，由于弧度和角度是一个相等的关系，只不过是两个不同的单位，最终我们可以推导出：

那么角度和弧度都可以换算出来：

（用弧度来表示1度）

（用度来表示1弧度）

在js中一弧度的写法：Math.PI/180；（π在javascript中是一个常量,用Math.PI表示）；

在实际开发中，我们更多的是想通过已知距离来推出角度，因为我们开发过程中经常需要获取距离，而且获取距离也是很容易获取的。这里我们需要介绍一个概念，反三角函数，推导过程如下：

1
2
3

sin(θ)=x/R ==== Math.sin( θ * Math.PI/180 )  =====》   θ = arcsin(x/R) ==== Math.asin(x/R)*(180/Math.PI)
cos(θ)=y/R ==== Math.cos( θ * Math.PI/180 )  =====》   θ = arccos(y/R) ==== Math.acos(y/R)*(180/Math.PI)
tan(θ)=x/y ==== Math.tan( θ * Math.PI/180 )  =====》   θ = arctan(x/y) ==== Math.atan(x/y)*(180/Math.PI)

这里的推导过程采取的是弧度制与角度之间的转换，其实最终的推导结果记住即可。

说了这么多数学知识，自己都烦了，现在我们看下如何在前端领域运用三角函数来解决问题，这里我们需要借助canvas来画图（下一篇文章我们重点介绍下canvas的使用案例）

星星移动案例

这个案例可以想象到现在的直播平台的点赞活动，无限点击，图标按照规律性的运动向上运动。

接下来看下简易效果:

想要实现这样一个效果，我们首先需要创建一个星星，同时绑定星星点击事件，代码如下：

 document.getElementById('star').onclick = function (e) {
    startPop(e)
}
 /*
    创建一个新的元素
 */
function createElement(e) {
    var star = document.createElement("div");
    var StarRandomSize = parseInt(Math.random() * 10 + 30);
    star.style.height = star.style.width = StarRandomSize + "px";
    var x = e.clientX;
    var y = e.clientY;
    star.style.color = randomColor();
    star.style.fontSize = StarRandomSize + "px";
    star.style.position = "absolute";
    star.style.left = e.currentTarget.offsetLeft + "px";
    star.style.top = y - StarRandomSize + "px";
    document.body.appendChild(star);
    star.innerText = "☆";
    return star
}

这里我们通过js创建一个元素为星星。完成了创建以后，最重要的是希望我们生成的这个星星向上飘动，同时希望他的飘动不是直线而是一种有规律性的飘动。这里我们就可以使用我们介绍的三角函数的特性来解决这个问题，不管是正弦，余弦，还是正切，他们的边界值都是[-1,1]之间，同时我们知道，三角函数的运动是呈规律性的，我们可以通过周期，振幅，图像的偏移量以及整个元素的位置来生成三角函数类型的规律性曲线。

这里我们结合上文中介绍的三角函数几个重要的参数，同时以正弦函数为例，来介绍下我们的设置，由于在计算机中是不能识别角度的，这里我们使用Math.PI/180来进行弧度制的转换，上文中已经介绍了角度转弧度的转换过程，这里我们直接使用，振幅来代表整个运动的幅度，这里不要设置太大，-2代表图形运动的偏移量。

1
2
3

function sinPath(deg) {
        return 10 * Math.sin(deg * Math.PI / 180 - 2)
}

知道规律以后，我们的想法是将三种运动函数，通过随机数的方式，使用tranform中的translate进行位移，进而可以将函数的规律和星星的运动进行了绑定。

var PathFun = [sinPath, tanPath, cosPath];
var RandomPathIndex = Math.round(Math.random() * 2);
moveY -=8;
star.style.transform = "translate(" + (PathFun[RandomPathIndex](deg) + "px") + "," + (moveY + "px") + ")"
function sinPath(deg) {
        return 10 * Math.sin(deg * Math.PI / 180 - 4)
}

function tanPath(deg) {
        return 2 * Math.atan(deg * Math.PI / 180)
}

function cosPath(deg) {
        return 10 * Math.cos(deg * Math.PI / 180)
}

如果需要让我们的元素运动起来，这个时候我们添加动画效果。我们计划采取requestAnimationFrame来解决这个问题，requestAnimationFrame其作用就是让浏览器流畅的执行动画效果。可以将其理解为专门用来实现动画效果的api，通过这个api,可以告诉浏览器某个JS代码要执行动画，浏览器收到通知后，则会运行这些代码的时候进行优化，实现流畅的效果，而不再需要开发人员担心刷新频率的问题了。

最终我们添加动画的代码如下：

var star = createElement(e);
var opacity = 100;
var deg = 0;
var PathFun = [sinPath, tanPath, cosPath];
var RandomPathIndex = Math.round(Math.random() * 2);
var moveY =0;
var start = null；
/*
    元素移动处理
*/
function step(timestamp) {
   if (!start) start = timestamp;
      opacity--;
      deg += 5;
      moveY -=8;
      star.style.transform = "translate(" + (PathFun[RandomPathIndex](deg) + "px") + "," + (moveY + "px") + ")"
      star.style.opacity = opacity / 100;
      if (star.style.opacity > 0) {
                window.requestAnimationFrame(step)
      } else {
                star.remove();
        }
      }
 window.requestAnimationFrame(step)

最终我们的动画就可以按照我们上面演示的那样进行显示了，这个案例不仅是介绍了整个星星的创建过程，同时我们在动画的位移中添加了三角函数的曲线规律，使得整个动画无论是从运动形式还是速率等一些特性上看起来更加符合我们视觉观察规律，从而运用数学的特性来解决了这个问题。

绘制水波图

有的时候我们经常能看到一个球里面有水波，这个水波曲线的实现其实也是和三角函数分不开的。先看下实现的一个粗略的效果:

实现过程

首先绘制一个标签，先绘制一个圆形，以此充当边框。这里我们采取canvas进行图形绘制，圆形绘制代码如下：

/// 创建一个圆形（只创建一次即可，不然影响动画性能）
ctx.beginPath();
const r = width / 2;
const h = height/2;
const lineWidth2 = 3;
const cR = r ;
ctx.arc(r, h, cR, 0, 2 * Math.PI);
ctx.stroke();
ctx.clip();
ctx.closePath();

绘制圆形最终要的属性是arc属性，arc相应参数如下：

根据参数表，我们设置这个圆形的X,Y坐标，同时计算圆的半径，使用 stroke()在画布上绘制圆弧。圆形绘制以后效果如下：

然后我们需要在圆形里面绘制波形图：

//绘制填充颜色
var lingrad = ctx.createLinearGradient(0,0,width,0);
lingrad.addColorStop(0, 'rgba(135,206,250)');
lingrad.addColorStop(1, 'rgba(240,255,255)');

ctx.clearRect(0, 0, width, height);
/// 创建第一个波形
ctx.beginPath();
ctx.fillStyle = lingrad;
ctx.lineWidth = 1;
// 设置起点位置
ctx.moveTo(0, height /2);

Q+=speed;

for (let x = 0; x <=  width; x++) {
    // 绘制的时候y跟着x跑即可。
    var y = A*Math.sin(W*x+Q) +H;
    ctx.lineTo(x, y);
    }
    ctx.lineTo(width, height);
    ctx.lineTo(0, height);
    ctx.fill();
    ctx.closePath();
}

上面代码中我们首先需要新建一个填充颜色，为了使得我们绘制的图形更加醒目我们需要设置一组渐变色来进行区分。我们根据y = 波浪高度 * sin(x * 波浪宽度 + 水平位移)来进行波浪的正弦函数的绘制。得到的效果图如下所示：

上面得到的是一个静态的函数图像，而我们一般见到的的波形图或水波都是随时间连续变化的，这里就要用到正弦函数中的参数相位Q，我们将Q随时间不断增加或减小，即可得到不同时间的不同图像；使用window.requestAnimationFrame实现帧动画；同时为了使得波浪看起来更加的没有规律性，使波形更自然，波形叠加一个频率更高的波形，使波形无规律。

代码如下：

var A=30,
    W=1 /180,
    Q=0,
    H= height / 2;
var speed=-0.10;
window.requestAnimationFrame(draw);
ctx.clearRect(0, 0, width, height);
/// 创建第一个波形
ctx.beginPath();
ctx.fillStyle = lingrad;
ctx.lineWidth = 1;
// 设置起点位置
ctx.moveTo(0, height /2);

Q+=speed;

for (let x = 0; x <=  width; x++) {
    var s = 0.1*Math.sin(x/200)+1;
      // 绘制的时候y跟着x跑即可。
      var y = A*Math.sin(W*x+Q) +H;
       y=y*s;
       ctx.lineTo(x, y);
    }
    ctx.lineTo(width, height);
    ctx.lineTo(0, height);
    ctx.fill();
    ctx.closePath();
}

效果如下：

这时候我们可以看到目前我们的波形已经按照一定的规律性运动起来了。单一的一条波形看着还是不太好看，我们为了优化可以再添加一条波形图。

// 创建第二个波形
var lingrad2 = ctx.createLinearGradient(0,0,width,0);
lingrad2.addColorStop(0,'rgba(240,255,255)');
lingrad2.addColorStop(1, 'rgba(135,206,250)');
ctx.beginPath();
ctx.lineWidth = 1;
ctx.fillStyle = lingrad2;

Q2+=speed2;
for (let x = 0; x < width; x++) {
        var y = A2*Math.sin(x*W2+Q2) +H2;
        ctx.lineTo(x, y);
}
ctx.lineTo(width,height);
ctx.lineTo(0,height);